Research

Slides for some of my talks can be found at Slideshare. I also have a (neglected) research blog.

My main research interests are about statistical inference for stochastic modelling, typically stochastic dynamical systems applied to biomedicine, Bayesian methods, Monte Carlo methods (MCMC, SMC).

I am particularly interested in statistical methodology for models not having a readily available likelihood function, that is so-called Simulation-Based Inference methods. Some of my favourite methods for intractable-likelihoods are found in the Bayesian framework, for example Approximate Bayesian Computation (ABC)

Other keywords related to my interests: inference for state-space models and stochastic differential equations (SDEs); accelerating MCMC computations for Bayesian inference; mixed-effects modelling for SDEs; stochastic modelling for tumor growth, protein folding and glycemia-insulinemia dynamics.

Below you can find short descriptions of some of the research areas and applications I have been involved with, together with links to the relevant publications (notice that most of my preprints are freely available in my publications page):

• Simulation-based inference methods (ABC and more)
• Mixed-effects models defined via SDEs
• Approximate maximum likelihood estimation
• Inference for large datasets and modelling of protein-folding
• Stochastic models for glycemia dynamics

© Christian P. Robert

Approximate Bayesian computation (ABC) is a Simulation Based-Inference (aka likelihood-free) methodology allowing inference for models having an "intractable likelihood" function (see a review by Sisson and Fan, 2010 and another review by Marin e al. (2011)). ABC circumvents the evaluation of the intractable likelihood function while still targeting an approximated posterior distribution. ABC methodology is fascinating and extremely flexible. Here I consider ABC for stochastic differential equation models observed with error. The case of partially observed systems is also considered. Simulations for pharmacokinetics/pharmacodynamics and for stochastic chemical reactions studies are presented. The abc-sde MATLAB package implementing the methodology is freely available.

In another paper with Julie Lyng Forman we used ABC for inference on a (relatively) large dataset and a computationally challenging sum-of-diffusions model for protein folding data.
In a joint work with Rachele Anderson we consider parameter estimation for a general class of models using an hybrid MLE-Bayesian strategy, ultimately leading to a maximum likelihood estimator while making use of an ABC-MCMC sampler: this work is based on the strategy popularly known as "data cloning".
In a joint work with Adeline Samson we embed ABC within SAEM (stochastic approximation EM) for maximum likelihood estimation in state-space models (also known as hidden Markov models).
A different likelihood-free methodology, named synthetic likelihood, was used for inference in stochastic differential mixed-effects models for tumor growth, and published in JRSS-C in 2019. Here is the preprint.
A main difficulty with ABC is how to construct informative summary statistics. In a paper accepted for ICML 2019, with Samuel Wiqvist, Jes Frellsen and Pierre-Alexander Mattei, we used deep learning to automatically construct these summaries for iid data and Markovian time series.
Together with Richard Everitt, we exploit stratified Monte Carlo to lower the variance of ABC likelihoods approximated via resampling schemes.
Together with Umberto Simola and Jukka Corander, we produce a novel MCMC proposal sampler for synthetic likelihoods. The proposed parameters are ``guided'' to produce simulated data that is close to observed data, resulting in a computationally more efficient MCMC algorithm. We also intoduce the notion of correlated synthetic likelihoods to increase the chains mixing.

Software: my abc-sde package

The picture above illustrate the fit of a mixed-effects SDE model to simulated data of five orange trees. For details go here.

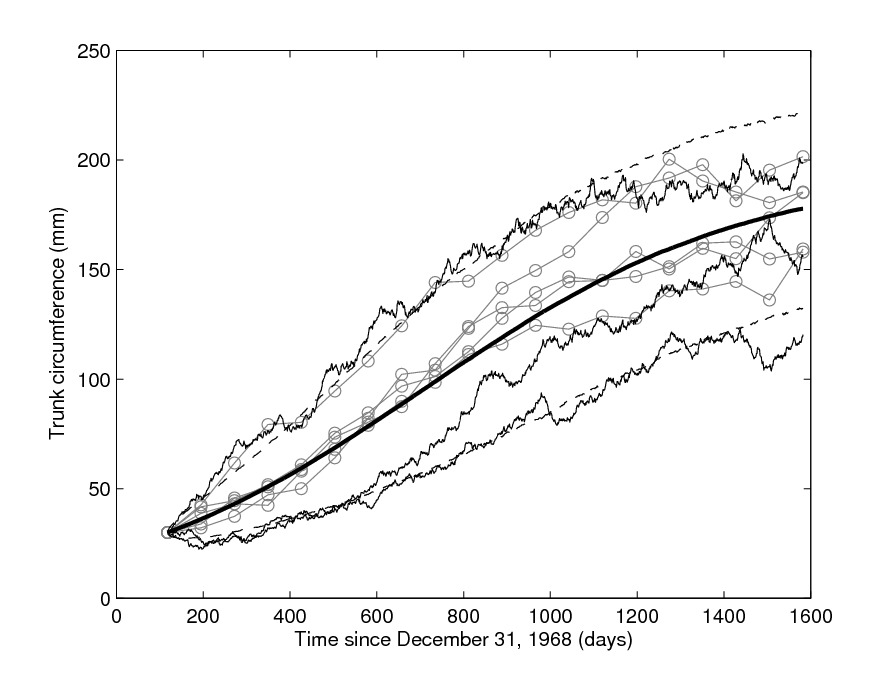It is often the case that a given experiment involves repeated measurements, particularly in biomedicine, where the several replicates might be measurements of the same experiment performed on different subjects or animals. Mixed-effects models assist in modelling variability when it is of interest to "catch" the overall behaviour of the entire "population" of subjects, that is making simultaneous inference for the collective dynamics of all subjects and not the individual (subject-specific) behaviour, by introducing random parameters. This allow for a more precise estimation of population parameters. This is especially interesting, and challenging, for mixed-models based on SDEs has been introduced: SDE mixed-effects models (SDEMEMs) allow the simultaneous representation of within-subject stochastic variability in addition to collective (between-subjects) variation. I have constructed novel frequentist and Bayesian inferential methods for SDEMEMs, see a methodological 2010 paper and a more computational paper from 2011 both with Andrea De Gaetano and Susanne Ditlevsen. See also an application to neuronal models.
With Julie Lyng Forman I have considered a "likelihood free" methodology named synthetic likelihood to estimate a stochastic model of tumor growth in mice, where different groups of mice are subject to different types of treatment.
With Samuel Wiqvist, Andrew Golightly and Ashleigh Mclean we have produced exact Bayesian inference for very general mixed-effects SDE models, including measurement error, using correlated particles pseudo-marginal methods. We believe that, to date, this is the most flexible methodology to efficiently handle inference for very general SDE mixed-effects models. A follow up paper introduces PEPSDI a framework for exact Bayesian inference using particle methods, suitable for many stochastic dynamical mixed-effects models with latent Markov dynamics, hence SDEMEMs are a special case. The code is written in the Julia language.

Approximate maximum likelihood estimation

"Likelihood-free" methods are of course also relevant outside the Bayesian paradigm considered above. A popular methodology for models having some hidden (unobserved) component is the EM algorithm for maximum likelihood estimation. An important implementation of EM is a stochastic version called SAEM (where the E-step in EM is approximated). While SAEM has nice algorithmic and theoretical properties, its application is restricted to models having an analytically tractable "complete likelihood" function. Also, SAEM requires from the user the analytic specification of sufficient statistics for such likelihood. This is typically impossible (or at best difficult) for most models of realistic complexity. In a single authored work I have enabled SAEM for complex intractable models, using the concept of synthetic likelihood. The resulting strategy is SAEM-SL, a "likelihood-free" version of SAEM (demo MATLAB code is available).
However, when the standard SAEM can be implemented (possibly after non-negligible effort) this can fail in some cases. For example, for the case of state-space models, with Adeline Samson we have shown how the popular bootstrap filter sequential Monte Carlo algorithm (which is a way to provide SAEM with paths for the latent process) can make SAEM produce very biased inference in some cases. A simple modification to such filter, involving an approximate Bayesian computation strategy, is able to produce better paths in some specific circumstances. See the resulting SAEM-ABC method and a MATLAB demo.

Software: MATLAB demo for SAEM-SL;   Software: MATLAB demo for SAEM-ABC

I have received a research grant from the Swedish research council for the interdisciplinary project "Statistical Inference and Stochastic Modelling of Protein Folding" (here is an accessible description) for which I am the principal investigator, in collaboration with Kresten Lindorff-Larsen (Dept. Biology, Copenhagen University) and Julie Lyng Forman (Dept. Biostatistics, Copenhagen University).
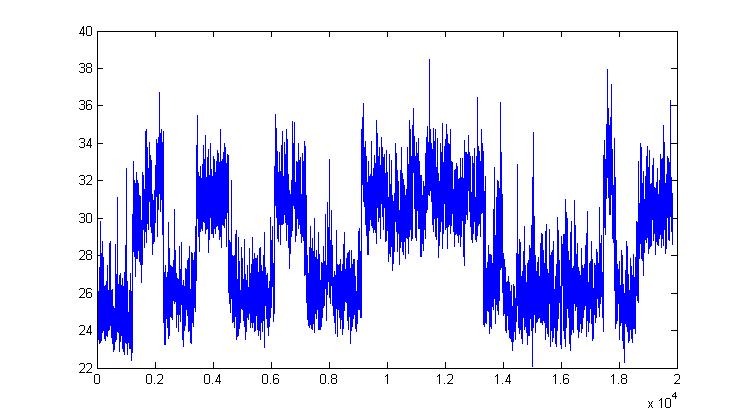
In a joint work with Julie Forman we have considered the problem of estimating folding rates for some protein having a coordinate switching between the folded and unfolded state, which is noticeable in the picture above. The so called "protein-folding problem" has been referred to as "the Holy Grail of biochemistry and biophysics" and therefore we are not contemplating to find a solution to this problem (!). However some contribution from the inference point of view can be given and we have proposed a new dynamical model (expressed as sum of two diffusions) and a quite fast computational strategy based on Approximate Bayesian Computation (ABC, see above) that seems to work well and could be used in place of exact Bayesian inference, when large datasets do not allow for the latter.
With Samuel Wiqvist and Julie Forman we have produced a new way to accelerate MCMC sampling, by exploiting tricks that accelerate the (already well studied) "delayed-acceptance" MCMC methodology. We basically find ways to avoid computing an expensive likelihood function. This has been applied with success to a dataset of 25,000 observations of a reaction-coordinate for protein folding data. We also propose a novel SDE double-well potential model who is able to reproduce the observed time-course accurately.

The picture above illustrate the fit of an SDE model to glycemia data. For details go here.

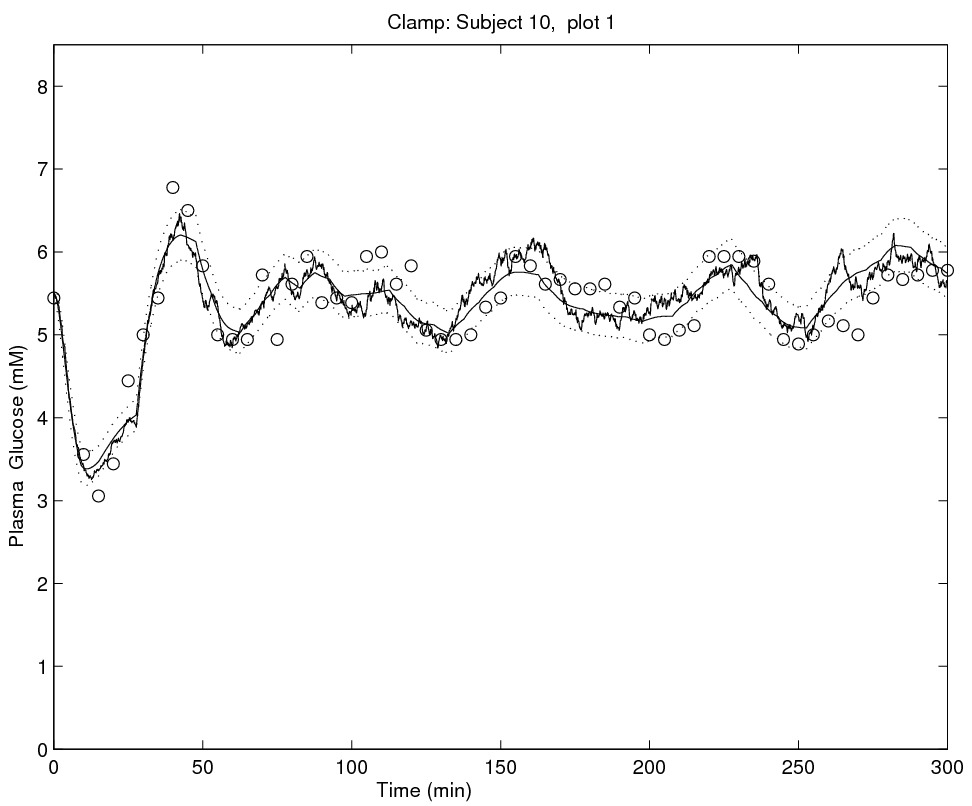In my early works, together with Andrea De Gaetano (Rome) and Susanne Ditlevsen (Copenhagen), I considered the problem of formulating models able to accommodate stochastic variability in glycemia dynamics. Previous attempts in literature focussed on deterministic modelling (ODE and DDE based), which are intrinsically unable to represent randomness in the modelled (physiological) system and thus the only random variability which could be contemplated had to be interpreted as measurement error. By using stochastic differential equations this is no more the case. In a 2006 paper we have been able to separately identify the intrinsic stochasticity in glycemia dynamics from measurement error variability. To ease the inference, a more computationally feasible model was proposed in a 2008 paper, where the likelihood function is approximated in closed form, but this time measurement error is not modelled.